So far, we’ve consistently placed the tonic (\(\hat{1}\)) on the note C. There are times, however, when it is desirable to move the tonic, and each of the other scale degrees, higher or lower to another pitch. Sometimes this helps bring a melody within a more comfortable range, other times it makes a melody playable on an instrument which would otherwise be unable to play it, and so on.
Transposing Melodies
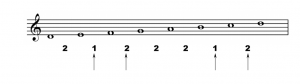
Suppose, for instance, that we want to move the tonic for “Frère Jacques” from C up to D. In order to make sure the melody sounds the same, we’ll have to be certain to keep all the intervals between its notes the same. To do this, let’s first write the first fourteen notes of “Frère Jacques,” labeling all of the intervals in terms of how many half steps they contain, with “+” indicating upward motion and “-” indicating downward motion.
If we want to move the starting pitch of “Frère Jacques” to D, just moving each of the pitches up to the next line or space does not maintain all of the original intervals. Note the arrows pointing to the intervals that don’t match the original melody:
In order to maintain all of the proper intervals, some of the pitches will have to be changed. The first interval, from D to E, is correct but the second, from E to F, is only one half step. In the original melody, it’s two half steps (a whole step), and we want to keep it that way to maintain the sound of the original tune. The note F must be moved up one half step in order for this to occur. The closest note above F which we’ve seen so far is G, but that’s a whole step above F, so we must invent a way to raise F one half step.
More than 800 years ago, musicians developed a symbol to raise any note one half step. It’s called a SHARP and looks like this: #.
On the musical staff, the sharp is always placed before the note it affects.
When speaking or writing in English, however, we say “F sharp” or write “F#”.
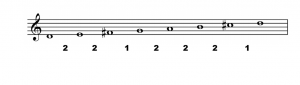
So now we can begin “Frère Jacques” on D, raise F to F#, and the first three notes will look like
If we continue to write out the tune, with D as the tonic, we find that every F must be raised to F# to make all the intervals correspond to the original:
Note that in measure 3 the interval between F# and G is one half step. That’s because the interval between F and G was a whole step, but by raising the F with a sharp we moved it one half step closer to the G.
By retaining the intervals of “Frère Jacques” while moving them to start on another pitch, we’ve TRANSPOSED it.
Transposing Scales
At this point, we could take “Frère Jacques” — and other melodies — and move them to various pitch levels. But there’s an easier way to gain a more global understanding of how the process of transposition works: If we transpose the major scale, we will transpose the pitches used in any melody based on the major scale.
Here is the major scale, with the number of half steps labeled between the successive pitches (review the intervallic definition of the major scale in Unit 3):
If we merely move each pitch up once, the interval content of the scale is not retained (the arrows mark the intervals that don’t match up with the major scale):
As in the transposed version of “Frère Jacques,” the F must be raised in order to correct the second and third intervals:
The intervals between B and C, and between C and D must also be corrected. To turn the interval between B and C into a whole step, the C must be raised one half step. By raising the C with a sharp, this also brings it to within one half step of the D, and thereby corrects this interval as well.
We now have two major scales: one that begins on C and the other on D. A scale is named by the pitch of its tonic (usually, the note on which it begins), so that these scales are named respectively the “C major scale” and the “D major scale.” if a piece of music is made up of the notes from the C major scale and has C as its tonic, it is said to be in the KEY of C major; if a piece is made up of the notes from the D major scale and has D as its tonic, it’s in the key of D major, and so on.
As you continue your work transposing scales, it will be important to remember an important principle of scale writing:
- Successive scale degrees should appear on successive lines and
spaces, and be named with successive pitch letter names. This
means that you should never skip a line or space or repeat notes
on any single line or space when writing scales on the staff.
As a practical matter, this means that — when writing scales — it’s best to write out the notes on successive lines and spaces first. Next, write out the intervals of the scale below and between them. Finally, check each interval — in succession from lowest to highest — and make the necessary changes to fit the intervals of the scale.
Let’s now transpose the major scale to begin on F. First, write out the notes on successive pitch letter names beginning with F:

Next, write the intervals of the major scale below and between them, and carefully check each interval — one by one — to see if they conform to those of the major scale.:
The first incorrect interval you’ll reach is the one between A and B: it should be a half step, but it’s a whole step. To bring these two notes closer together, you could try raising the A with a sharp, but this would disturb the whole step between G and A. The B is the note which must be altered: it must be lowered one half step.
To lower a note by a half step, musicians use a symbol called a FLAT, which
looks like this: \(\flat\).
Exactly like the sharp, we place the flat symbol before the note on the staff, but we say “B-flat” or write “B\(\flat\) ”
Returning to our F-major scale, if we add a flat to the B it will bring it to within one half step of the A and thereby correct the interval between them. Lowering the B also moves it one whole step away from C, thereby correcting the fourth interval as well. (There is a natural half step between B and C, and lowering the B moves it one more half step away.)
After checking the remaining intervals, you’ll find that they are all correct just as they are. Here, then, is the F-major scale:
Tendency Tones
In Western Classical music, the scale can be used to create tension and forward motion in melodies and harmonies. Specifically: in this repertoire, the scale’s half-steps are used as “tendency tones,” with scale-degree 7 tending to move toward scale-degree 1, and scale-degree 4 tending to move toward scale-degree 3. This means that if a melody emphasizes scale-degree 7, for instance, it will have a tense feel until that melody moves to scale-degree 1. (We will return to how listeners learn to associate these tones with certain expectations in later units.)
Enharmonic Pitches
The sharp and the flat may be applied to any note, so that D, for instance, may be raised or lowered. This gives rise to a curious principle in music. In the interval between two notes a whole step apart, you may find an additional note by adding a sharp to the lower note and by adding a flat to the higher note. Since they each move one half step to the center, they meet at what is for our present purposes the same pitch.
For example, the distance between C and D is one whole step. By raising C to C# you bring it to within one half step of D. If you then lower D to Db, it will move down one half step to meet this C#. The two notes will sound alike, but this one pitch has two different names. When two names are used for the same pitch, the names are said to be ENHARMONIC.
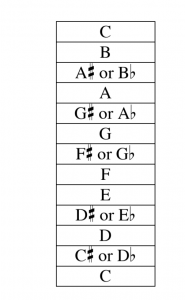
Between any two pitches a whole step apart there is a pitch with two enharmonic names. We can now write out the names for all the pitches on successive half steps.
First, we’ll write them as a vertical list:
We can also write this list of pitch names on the staff:
On the staff list above, the unaltered letter names have been written alone in their own separate measures, and the enharmonic pitches achieved through sharps and flats have been written in pairs in the other measures.
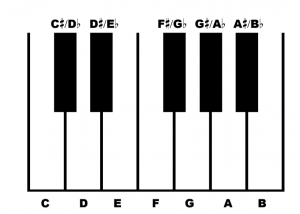
We can also show how these notes correspond to the keys of the piano: